3025: Find the Number of Ways to Place People I
Problem Statement
You are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D plane, where points[i] = [xi, yi].
Count the number of pairs of points (A, B), where
Ais on the upper left side ofB, and- there are no other points in the rectangle (or line) they make (including the border).
Return the count.
Example 1:
Input: points = [[1,1],[2,2],[3,3]]
Output: 0
Explanation:
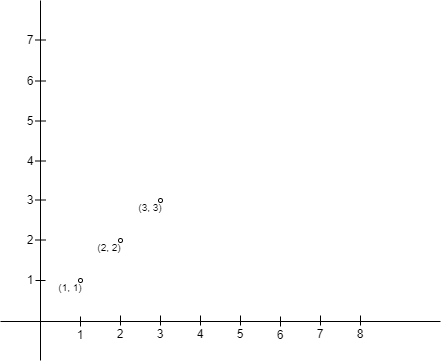
There is no way to choose A and B so A is on the upper left side of B.
Example 2:
Input: points = [[6,2],[4,4],[2,6]]
Output: 2
Explanation:
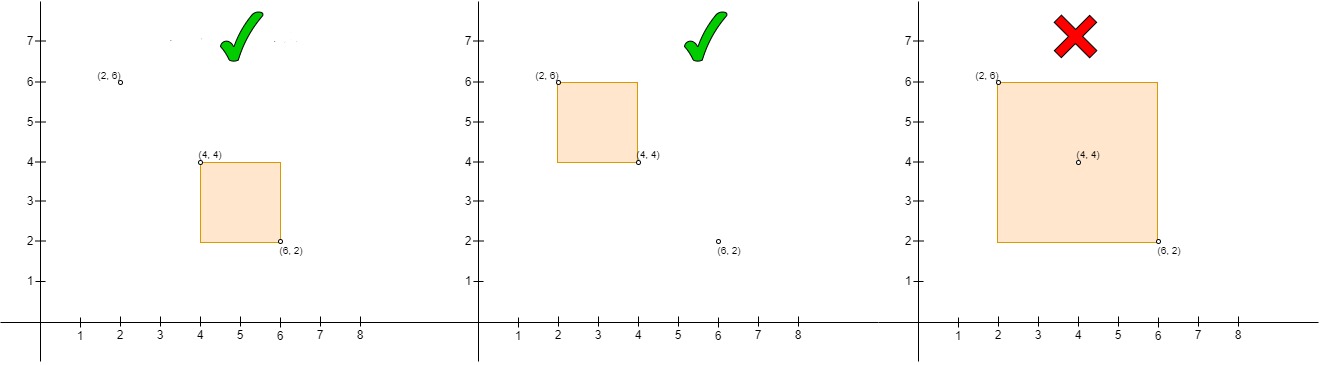
- The left one is the pair
(points[1], points[0]), wherepoints[1]is on the upper left side ofpoints[0]and the rectangle is empty. - The middle one is the pair
(points[2], points[1]), same as the left one it is a valid pair. - The right one is the pair
(points[2], points[0]), wherepoints[2]is on the upper left side ofpoints[0], butpoints[1]is inside the rectangle so it's not a valid pair.
Example 3:
Input: points = [[3,1],[1,3],[1,1]]
Output: 2
Explanation:
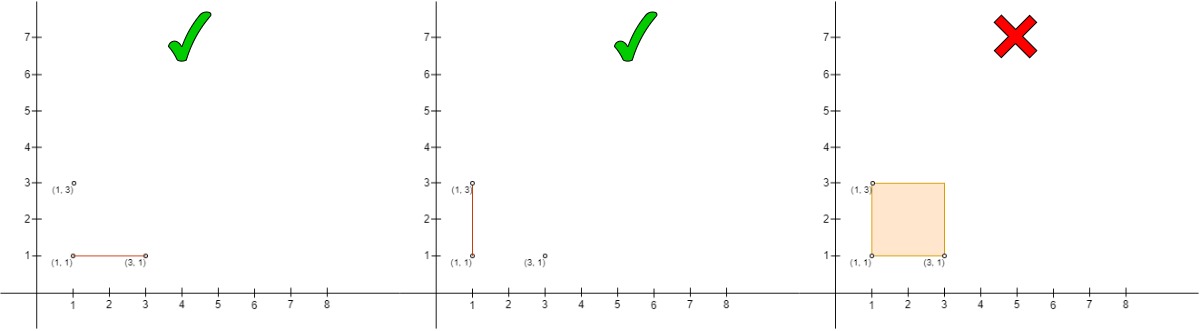
- The left one is the pair
(points[2], points[0]), wherepoints[2]is on the upper left side ofpoints[0]and there are no other points on the line they form. Note that it is a valid state when the two points form a line. - The middle one is the pair
(points[1], points[2]), it is a valid pair same as the left one. - The right one is the pair
(points[1], points[0]), it is not a valid pair aspoints[2]is on the border of the rectangle.
Constraints:
2 <= n <= 50points[i].length == 20 <= points[i][0], points[i][1] <= 50- All
points[i]are distinct.
Code Solution