3620: Network Recovery Pathways

Problem Statement

You are given a directed acyclic graph of n nodes numbered from 0 to n − 1. This is represented by a 2D array edges of length m, where edges[i] = [ui, vi, costi] indicates a one‑way communication from node ui to node vi with a recovery cost of costi.

Some nodes may be offline. You are given a boolean array online where online[i] = true means node i is online. Nodes 0 and n − 1 are always online.

A path from 0 to n − 1 is valid if:

  • All intermediate nodes on the path are online.
  • The total recovery cost of all edges on the path does not exceed k.

For each valid path, define its score as the minimum edge‑cost along that path.

Return the maximum path score (i.e., the largest minimum-edge cost) among all valid paths. If no valid path exists, return -1.

Example 1:

Input: edges = [[0,1,5],[1,3,10],[0,2,3],[2,3,4]], online = [true,true,true,true], k = 10

Output: 3

Explanation:

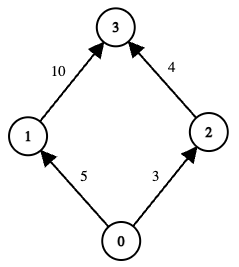
  • The graph has two possible routes from node 0 to node 3:

<ol data-end="462" data-start="209">
	<li data-end="315" data-start="209">
	<p data-end="228" data-start="212">Path <code>0 &rarr; 1 &rarr; 3</code></p>

	<ul data-end="315" data-start="234">
		<li data-end="315" data-start="234">
		<p data-end="315" data-start="236">Total cost = <code>5 + 10 = 15</code>, which exceeds k (<code>15 &gt; 10</code>), so this path is invalid.</p>
		</li>
	</ul>
	</li>
	<li data-end="462" data-start="318">
	<p data-end="337" data-start="321">Path <code>0 &rarr; 2 &rarr; 3</code></p>

	<ul data-end="462" data-start="343">
		<li data-end="397" data-start="343">
		<p data-end="397" data-start="345">Total cost = <code>3 + 4 = 7 &lt;= k</code>, so this path is valid.</p>
		</li>
		<li data-end="462" data-start="403">
		<p data-end="462" data-start="405">The minimum edge‐cost along this path is <code>min(3, 4) = 3</code>.</p>
		</li>
	</ul>
	</li>
</ol>
</li>
<li data-end="551" data-start="463">
<p data-end="551" data-start="465">There are no other valid paths. Hence, the maximum among all valid path‐scores is 3.</p>
</li>

Example 2:

Input: edges = [[0,1,7],[1,4,5],[0,2,6],[2,3,6],[3,4,2],[2,4,6]], online = [true,true,true,false,true], k = 12

Output: 6

Explanation:

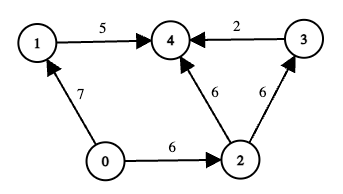
  • Node 3 is offline, so any path passing through 3 is invalid.

  • Consider the remaining routes from 0 to 4:

<ol data-end="1231" data-start="840">
	<li data-end="985" data-start="840">
	<p data-end="859" data-start="843">Path <code>0 &rarr; 1 &rarr; 4</code></p>

	<ul data-end="985" data-start="865">
		<li data-end="920" data-start="865">
		<p data-end="920" data-start="867">Total cost = <code>7 + 5 = 12 &lt;= k</code>, so this path is valid.</p>
		</li>
		<li data-end="985" data-start="926">
		<p data-end="985" data-start="928">The minimum edge‐cost along this path is <code>min(7, 5) = 5</code>.</p>
		</li>
	</ul>
	</li>
	<li data-end="1083" data-start="988">
	<p data-end="1011" data-start="991">Path <code>0 &rarr; 2 &rarr; 3 &rarr; 4</code></p>

	<ul data-end="1083" data-start="1017">
		<li data-end="1083" data-start="1017">
		<p data-end="1083" data-start="1019">Node 3 is offline, so this path is invalid regardless of cost.</p>
		</li>
	</ul>
	</li>
	<li data-end="1231" data-start="1086">
	<p data-end="1105" data-start="1089">Path <code>0 &rarr; 2 &rarr; 4</code></p>

	<ul data-end="1231" data-start="1111">
		<li data-end="1166" data-start="1111">
		<p data-end="1166" data-start="1113">Total cost = <code>6 + 6 = 12 &lt;= k</code>, so this path is valid.</p>
		</li>
		<li data-end="1231" data-start="1172">
		<p data-end="1231" data-start="1174">The minimum edge‐cost along this path is <code>min(6, 6) = 6</code>.</p>
		</li>
	</ul>
	</li>
</ol>
</li>
<li data-end="1314" data-is-last-node="" data-start="1232">
<p data-end="1314" data-is-last-node="" data-start="1234">Among the two valid paths, their scores are 5 and 6. Therefore, the answer is 6.</p>
</li>

Constraints:

  • n == online.length
  • 2 <= n <= 5 * 104
  • 0 <= m == edges.length <= min(105, n * (n - 1) / 2)
  • edges[i] = [ui, vi, costi]
  • 0 <= ui, vi < n
  • ui != vi
  • 0 <= costi <= 109
  • 0 <= k <= 5 * 1013
  • online[i] is either true or false, and both online[0] and online[n − 1] are true.
  • The given graph is a directed acyclic graph.

Code Solution